Research
My academic career started in algorithm theory and engineering, especially in computational geometry and topology, with links to CAD/CAM, machine learning and security. Later my focus shifted to artificial intelligence and system architectures for industrial control systems. During my time in industry I worked in a broader sense on smart factory technology.
I am the director of the Josef Ressel Center for Intelligent and Secure Industrial Automation, with research fields on system architectures, artificial intelligence and security for industrial automation.
Current research
-
Industrial system architectures
We investigated SOAs, digital twins, RAMI4.0-related and machine learing-related topics in the design of modern industrial software and system architectures, partly based on real-world testbeds and demonstrators. More to come…
-
Computational topology for industrial applications
We are interested in the application of computational topology (in particular persistent homology) in industrial applications, e.g., anomaly detection based on state space trajectories of industrial machines. More to come…
-
Cybersecurity for industrial systems
We are interested in threat modeling, the design of security architectures, methods for intrusion detection and the design of honey pots, all being suitable for industrial control systems (operation technology). More to come…
-
TensorFlow-based spline optimization
Modern machine learning frameworks, like TensorFlow, possess a battery of modern numerical optimizers in order to train neural nets. These can be used to reinvestigate classical optimiaztion problems in mechatronics, like particular spline approximations, say, for cam profile generation. More to come…
-
AI-based optimizations for industrial systems.
We are interested in meta-heuristics (e.g., genetic programming) for optimization problems. For instance, we exploit symmetries of the solution space of the Traveling Salesperson Problem from an algebraic point of view for a general construction scheme to enhance crossover operators for genetic algorithms. As another example, we investigate Reinforcement Learning for mechatronic motion planing problems. More to come…
Previous research
-
The KI-Net project is an Interreg research project in which we broadly investigate methods of artificial intelligence and related methods in the application domain of manufacturing. This project is lead by SCCH with Univ. of Innsbruck, HS Kempten, TH Rosenheim and FH Salzburg as consortial partners.
Besides original research the main focus at Interreg projects is at the dissemination and demonstration of prototypes with a focus on SMEs. More…
-
In order to address challenges of modern production of goods in discrete industrial automation, such as batch size one production, mass customization and flexible product changeovers, we require transport systems within and between machines that combine servo-like motion control, robot-like multi-axis coordination and complex material flow topology.
Within this cooperate research project during my industry appointment at B&R Industrial Automation, we developed a novel lang-stator linear motor system ACOPOStrak, which accommodates a flexible number of shuttles that realize complex patterns of material flow yet trivial to operate for the application engineer. Furthermore, we have to establish mechanisms that shift the focus from motion control programming to shuttle-agnostic process programming. More…
-
For certain machine learning tasks topological information of data has been proven valuable. Persistence diagrams are a prominent way to summarize topological information of data gained from persistent homology.
Recently, we developed a so-called positive definite kernel on the space of persistent diagrams, which enables the application of many established machine learning tools (e.g., support vector machines, k-means, principle component analysis) on persistence diagrams. We thereby establish a bridge between topological data analysis and machine learning. More…
-
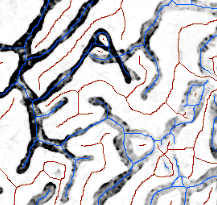
The lymphatic system of vertebrates is part of the circulartory system. It drains fluid from the body’s tissue in order to get reabsorbed into the blood vessels.
The biological mechanisms that govern the growth of lymph vessels are essentially unkown. In cooperation with Kari Vaahtomeri, Michael Sixt and Herbert Edelsbrunner, we attempt to gain insight into these mechanisms by investigating topological, geometric and statistical properties of the lymph vessel shapes using tools from computational topology and geometry.
-
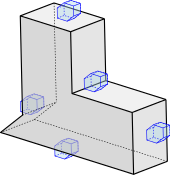
Higher-dimensional straight skeletons
Since 2008, different attempts to develop a definition of straight skeletons of polyhedra in three-space were proposed.
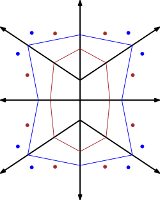
Our contribution towards a generalization to straight skeletons of polyhedral bodies of arbitrary dimension relies on Voronoi diagrams in normed spaces with a suitable polyhedral norm (blue) for a class of polyhedral input shapes (black) that lies dense in the set of all polyhedral bodies. The solid foundation of Voronoi diagrams allows us to bypass the difficulties faced in prior attempts that go directly for a definition of the structure of the so-called straight-skeleton wavefront. More…
-
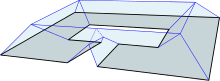
The straight skeleton of a polygon gives rise to a corresponding (hip) roof whose facets have unit slope. The (multiplicatively) weighted straight skeletons correspond to roofs with facets of arbitrary slope – the (reciprocal) weights of the polygon edges. Negative weights, for instance, cause overhanging roof-facets, which has far-reaching implications for the geometric, combinatorial and topological properties of straight skeletons, its faces and the roof models. More…
-
We ask the reversed question of computing the Voronoi diagram or the straight skeleton of some input. That is, given a tessellation of the plane into polygonal cells - is this the straight skeleton or the Voronoi diagram of some input? And if yes, can we (efficiently) reconstruct the input? And how can we (efficiently) determine the set of all possible inputs, in case that the reconstruction is not unique?
These questions are partly motivated by applications in biology, but also have theoretical and practical implications in computational geometry. More…
-
Straight skeletons and motorcycle graphs
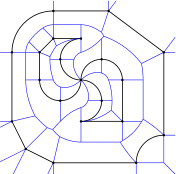
The straight skeleton (blue) of a straight-line figure (black) is a geometric structure that was introduced to computational geometry in the mid 90s. Similar to Voronoi diagrams, it is used in a multitude of applications in science and industry, such as computing mitered offset curves (red), automatic generation of tool paths in NC machining, solving mathematical origami problems or reconstructing 3D bodies in medical imaging. A motorcycle graph is a geometric structure that is strongly related to the straight skeleton in different ways. More…
-
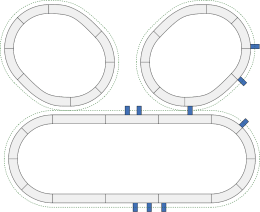
Watermarking refers to a process of embedding imperceptible statistical features into a digital asset (e.g., music, movies, vector graphics) that can be detected by those who possess a specific secret key. This enables the owner of a watermarked digital asset, such as geographic maps or a CAD drawing, to prove his ownership or retrace which collaborator illegitimately passed on the asset. More…
-
Voronoi diagrams and their generalizations are key objects in computational geometry and have been thoroughly investigated in the past four decades. Voronoi diagrams of straight-line segments are heavily used in science and industry and a few Voronoi-implementations are available that can cope with real-world datasets. For Voronoi diagrams of points, straight-line segments and circular arcs, however, ArcVroni is to our knowledge still the only implementation that is able to run on an industrial-strength level. More…