Inverse problems

Introduction. The Voronoi diagram¹ of points or the straight skeleton² of a PSLG³ can itself be interpreted as a PSLG (with some infinite edges pointing to a vertex at infinity). Hence, we can ask for any given graph G whether G can be realized as a Voronoi diagram or a straight skeleton. Depending on how much geometric information of G is given we end up with different problems.

Abstract graphs. It has been shown by Dillencourt⁴ and Dillencourt and Smith⁵ that every 4-connected planar graph and every outer-planar graph can be realized as the Voronoi diagram of points. In [Aic*12b] we showed that every tree can be realized as the straight skeleton or the Voronoi diagram of a convex polygon. In [Aic*15] we gave sufficient and necessary conditions for a directed tree to be the (directed) straight skeleton of a polygon. (The direction of an edge of the straight skeleton is given by the direction of the wavefront propagation.)

Phylogenetic trees. Cheng et al.⁶ motivated the question of realizability of phylogenetic trees as the straight skeleton polygons. Here not only the structure of the tree is given but also the lengths of the edges and the incidence orders of the vertices. That is, one is allowed to rotate edges of the trees, as long as the incidence orders and the edge Lent’s are preserved.

Hence, the problem could also be stated as follows: Can we rotate the edges at the inner vertices in a way that the straight skeleton of the polygon that results from cyclically connecting the leaf nodes is identical to the tree? In [Aic*12, Aic*12b] we gave a method that checks whether a (phylogenetic) caterpillar graph⁷ can be realized. We showed that there can be zero but at most finitely many realizations and we gave a construction scheme for suitable polygons. In the worst case at least an exponential number of realizations may exist, even for caterpillar graphs. For general phylogenetic trees the problem is still open. It is even unclear whether there can be infinitely many realizations for a general phylogenetic tree.

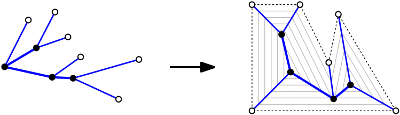
Geometric graphs. In [BHH*13, BHH*13b] we asked whether a PSLG G can be realized as the straight skeleton of a PSLG H. That is, the locus of each vertex of G is fixed. (In [BHH*13] we considered the special case where G is a tree with the leaf-edges extended to infinity.)

We started with a characterization of straight skeletons, which also allows to implement O(n) a-posteriori validity checks in straight-skeleton implementations. The central vehicle for the recognition problem of straight skeletons as a framework that successively reflects faces of G and suitable supporting lines of edges of potential graphs H along a spanning tree of the dual of G to a designated face of G. This allows us to tackle to problem simultaneously in all cells of G. At the end we can compute a representation of all possible solutions H in O(n log n) time, where n denotes the number of edges of G.

It turns out that the very same technique can also be used to determine all possible point sets whose Voronoi diagram is equal to G in O(n log n) time. Hence, our framework fills a gap in the paper by Ash and Bolker⁸, which required the assumption that all vertices of G are of odd degree.

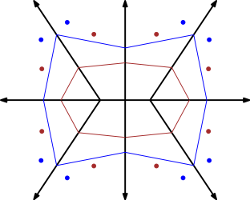
In the following figure the red point set, the blue point set, the red polygon and the blue polygon each realize the same Voronoi diagram and straight skeleton, respectively.