Straight skeletons and motorcycle graphs

Introduction. The straight skeleton of a simple polygon is, like the Voronoi diagram, a tree structure within the polygon. It has been introduced to computational geometry in the mid-90s by Aichholzer et al.¹ and its definition is closely related to mitered-offset curves.

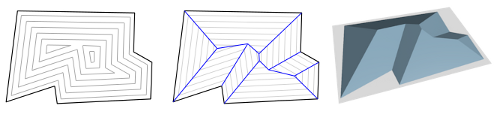
Consider the black polygon above. The gray sub-polygons show a wavefront process where every edge is moving inwards with constant speed. And while this wavefront propagates some edges may vanish and other edges may split, until the wavefront vanishes. If you trace the movement of every wavefront vertex, you obtain the straight skeleton (blue). This definition was later extended from polygons to planar straight-line graphs.

Aichholzer et al. also gave a different way of looking at the straight skeleton: If we embed the wavefront propagation into three-dimensional space where the z-axis is time, then the wavefront traces out a three-dimensional roof shape. This is the so-called terrain model or roof model as shown in the right subfigure.

Applications. Similar to Voronoi diagrams, straight skeletons have a lot of applications in different research areas. An incomplete list comprises:

• Computing mitered offset curves and tool-path generation in CAD/CAM.
• Shape reconstruction and contour interpolation of three-dimensional bodies, e.g., in medical imaging.
• Automatic generation of hip roofs and variants for buildings.
• Landscape generation of mountain terrain.
• Solving fold-and-cut problems in the field of mathematical origami.
• Topology-preserving map simplification and extraction of center-lines of roads in geographic information systems.

A comprehensive overview on the research of straight skeletons and motorcycle graphs up to the year 2011 is given in my book Computing Straight Skeletons and Motorcycle Graphs: Theory and Practice published at the Shaker Verlag:

Our contribution.

• Computing motorcycle graphs. A motorcycle graph is a geometric structure that is in a close relationship with straight skeletons.

  In [HuHe09, HuHe11b] we presented an algorithm for computing motorcycle graphs based on geometric hashing. A stochastic analysis shows that on average the algorithms runs in O(n log n) time if the motorcycles are distributed uniformly enough. Outside the convex hull of the start points of the motorcycles the algorithm runs in deterministic O(n log n) worst case time. The resulting implementation MOCA has been extensively tested and shows an O(n log n) runtime for the vast majority of input files in our database of 22.000 datasets of various characteristics, including industrial data.

  In [MHH12] we investigated kinetic triangulations in order to compute motorcycle graphs. The main advantage of this approach is that its runtime is less sensitive to the distribution of the motorcycle. Experimental results (the implementation was done by Willi Mann) show virtually no outliers from an O(n log n) runtime behavior.

• Triangulation-based algorithm. Aichholzer and Aurenhammer² presented a straight-skeleton algorithm that simulates the wavefront by means of a kinetic triangulation. A big open problem is the exact worst-case runtime complexity of this algorithm, which is known to be somewhere between O(n³ log n) and O(n² log n).

  In [HuHe10], we investigated the number of so-called flip events in these kinetic triangulations. We were able to show that polygons exist where a linear number of diagonals are flipped each a linear number of times. Furthermore, polygons exist where every triangulation leads to a quadratic number of flip events and even retriangulating does not help to save computing time. The most import result is, however, that Steiner triangulations of polygons exist were no flip events exist at all.

  While the best known bound for the worst-case time complexity is still O(n³ log n), it has been unclear how well this algorithm would actually perform for practical input data. In [PHH12], we report on experimental results of an carefully engineered implementation of this algorithm by Peter Palfrader. It turned out that some non-trivial algorithmic gaps needed to be filled in order to actually turn the algorithm into an implementation.

• Motorcycle graphs and straight skeletons. In [HuHe11c], we proved that a motorcycle graph can be simulated by straight skeletons. This is interesting as lower bounds of motorcycle graphs can therefore be transferred to straight skeletons. In particular, the P-completeness of straight skeletons follows from the P-completeness of motorcycle graphs. Hence, there are no efficient parallel algorithms for straight skeletons. These results were already mentioned by Eppstein and Erickson³.

  In [HuHe11, HuHe12], we proved that the straight skeleton of an arbitrary planar straight-line graph can be defined as the lower envelope of partially defined linear functions via a generalization of the motorcycle graph. This result generalizes partial results by Eppstein and Erickson³ resp. Cheng and Vigneron⁴. As a result, the straight skeleton can be computed by means of graphics hardware using a similar technique as Hoff et al.⁵ describes for Voronoi diagrams.

  This result also forms the foundation for our straight-skeleton algorithm and its implementation STALGO. STALGO was the first implementation that ran in O(n log n) runtime for practical input data on an industrial-strength reliability level. Compared to the straight-skeleton code in CGAL, STALGO is by a linear factor faster and uses by a linear factor less memory. For datasets with a 10.000 vertices, STALGO runs by two to three orders of magnitudes faster and uses less than 100 Mb of RAM, instead of 10 GB.