Generalized Voronoi diagrams

Introduction. Voronoi diagrams of points in the Euclidean plane were first defined one and a half centuries ago by Lejeune Dirichlet when investigating quadratic forms.¹ Besides the basic Voronoi diagrams of points, various generalizations have been of interest in the field computational geometry:²

• Voronoi diagrams in higher-dimensional spaces.
• Voronoi diagrams in spaces endowed with different metrics and distance functions.
• Voronoi diagrams of not just points but various types of geometric objects.

All these kinds of Voronoi diagrams have in common that we consider a finite set of input objects. Then the Voronoi diagram of these objects tessellates the space into so-called Voronoi cells such that (i) every Voronoi cell uniquely belongs to an object and (ii) the Voronoi cell of an object A comprises those points that are closer to A than to any other object B.

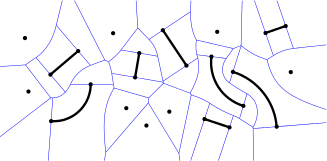
Voronoi diagram of points, straight-line segments and circular arcs. In Held and Huber [HeHu08, HeHu09], we generalized the topology-oriented approach of Sugihara and Iri³ in order to compute the Voronoi diagram of points, straight-line segments and circular arcs. The resulting implementation ArcVRONI is an extension to Held’s VRONI, which adds circular arcs to the list of supported input primitiva.

To our knowledge, ArcVRONI is still the only available Voronoi code that is able to compute the Voronoi diagram of points, straight-line segments and circular arcs on an industrial-strength level. ArcVRONI is available for commercial and academical use and, in fact, has been licensed for many industrial applications. Besides Voronoi diagrams, ArcVRONI also features the computation of the medial axis and offset curves based on Minkowski-sums.

For more details on VRONI, ArcVRONI, industrial and scientific applications of Voronoi diagrams, and example figures I refer to Martin Held’s website.

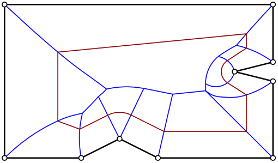
Variable-radius Voronoi diagram. In [HHP16, HHP15b,HHP15], we further generalized Voronoi diagrams in the following way: Similar to straight skeletons, one can define Voronoi diagrams as the interference pattern of a propagating wavefront⁴. The wavefront is an offset curve that is based on Minkowski sums with disks of a fixed radius. In this sense, the wavefront grows everywhere at unit speed. We generalized the wavefront process to non-uniform speeds and, in return, get as the dual skeleton structure a generalized Voronoi diagram, which we call variable-radius Voronoi diagram.