Weighted straight skeletons

Introduction. The definition of the straight skeleton of a simple polygon is based on a wavefront that is emanated from the polygon. In the picture below, the vertices of the wavefront (gray) trace out the straight skeleton (blue), which forms a tree structure within the polygon. this definition can be applied to polygons with holes too, in which case each hole gives rise to a cycle in the straight skeleton.

If we embed the propagation process of the wavefront in three-space, where the z-axis depicts time, then the wavefront traces out the so-called roof model (right-most picture) of the polygon.

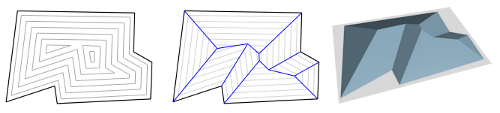
For the (ordinary) straight skeleton, the wavefront edges all move at unit speed. The weighted straight skeleton is a generalization of the (ordinary) straight skeleton where the wavefronts edges may propagate at any constant speed. Consequently, the inclination of the facets of the roof model to the ground plane is not necessarily 45°.

Prior work. Weighted straight skeletons were applied in geographical information systems¹, in automatic roof construction², or the design of pop-up cards³. They are also used in a generalization of straight skeletons to polyhedra in three-space in order to define the initial wavefront structure.⁴ An \(O(n^{8/5 + \epsilon})\) algorithm was presented in 1999 by Eppstein and Erickson⁵.

Ambiguities, geometry, combinatorics, topology. Algorithms, applications and even simple implementations already existed for weighted straight skeletons when only little was known about the skeleton itself. In particular, a proper definitions was still missing, while it was silently assumed that the weighted straight skeleton behaves more or less similar to the unweighted one.

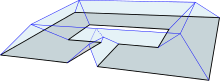
In [Bie*15, Bie*13] we shed light on the ambiguity of the intuitive definition mentioned above and proposed resolving strategies. We investigated geometric, combinatorial and topological properties of the weighted straight skeletons and compared those with the unweighted case. For instance, even for a convex polygon the weighted straight skeleton can have crossings. The following figure shows a simple example of a simple polygon whose weighted straight skeleton has cycles and its roof may be topologically equivalent to a doughnut:

A proper definition via a stable roommates problem. In [BHP16, BHP14b, BHP14] we presented the first rigorous definition of weighted straight skeletons. We first put the previous definition of so-called events (i.e., changes in the wavefront structure) on a new foundation that employs a topological point of view. As a side result, we end up with a unified definition of events, where the subsequent distinction of edge events, split events, vertex events, and so on is superfluous.

The structural adaptions of the wavefront in course of the event handling express themselves as edge-pairing problems. We translated the edge-pairing problem to a so-called planar matching problem in a pseudo-line arrangement, which we introduced in [BHP16, BHP14b, BHP14]: We are given an even number of directed lines (black), where each line enters and exits a disk (gray) exactly once, each pair of lines intersects exactly once, and no triple intersects. A planar matching is a pairing of the lines such that the segments (blue) of the lines from the entry points to the intersection points with its pairing mates do not intersect, except where they meet the pairing mate:

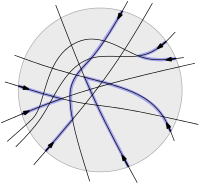
We showed that the planar matching always exists by further translating it into a stable roommates problem.

Algorithms. Only a few results are known about algorithms of weighted straight skeletons. We showed in [Bie*15, Bie*13] that for positive weights the weighted straight skeleton behaves combinatorially and topologically basically the same as the unweighted straight skeleton. Eppstein and Erickson⁵ gave in 1999 an \(O(n^{8/5+\epsilon})\) time and space algorithm for positively⁶ weighted straight skeletons.⁷ For monotone polygons and positive weights, we gave in [Bie*15b, Bie*14] an algorithm that runs in \(O(n \log n)\) time and \(O(n)\) space.⁸ For convex polygons and arbitrary weights the weighted straight skeleton can be computed in optimal \(O(n)\) time [Bie*15].