Voronoi diagram of a convex polyhedron
In this little blog article, we will show how the Voronoi diagram of a convex polyhedron \(P\) in \(d\)-dimensional Euclidean space can be computed in \(O(n^{\lceil \frac{d}{2} \rceil} + n \log n)\) time. As the attentive reader might guess by the time complexity, this is done by intersecting \(n\) half-spaces in \(\mathbb{R}^{d+1}\).
Preliminiaries. The Voronoi diagram of \(n\) sites1 tessellates space into \(n\) so-called Voronoi cells, each of which consisting of those loci that are closer to the defining site than to any other. When we speak of the Voronoi diagram of a polyhedron \(P\), then we consider the set of faces of \(P\) as the set of sites. Also, we are here only interested in the Voronoi diagram within \(P\).2 Below we see the Voronoi diagram (blue) of a polygon (black), i.e., a polyhedron in the plane:
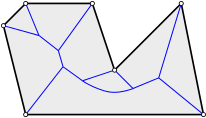
Each face of \(P\) has a Voronoi cell that is bounded by blue lines and its defining site (as we restricted the Voronoi diagram to \(P\)). The Voronoi diagram consists of loci that are equidistant to two sites. Hence, it is made of pieces of straight lines and parabolas in the plane, resp. quadrics in higher-dimensional space.
Convex polyhedra. The Voronoi cells of the convex vertices are collapsed to a point. This observation can be generalized:
Lemma. If \(P\) is a convex polyhedron3 then only its facets4 have Voronoi cells with non-empty interior.
Proof. Consider a point \(p\) in the interior of \(P\). It suffices to show that all closest5 faces of \(P\) to \(p\) are facets. Assume to the contrary that \(F\) is closest and \(i\)-dimensional, with \(0 \le i \le d-2\), and let \(r\) be the distance. Then the ball \(B\) centered at \(p\) and with radius \(r\) does not intersect \(P\) in its interior, but touches \(F\) in a point \(q\). Hence, a local neighborhood at \(q\) on \(P\) is contained in the tangential hyper-plane at \(q\) on \(B\). In other words, \(F\) is flat, which is a contradiction.
From this lemma it follows that we only need to consider the facets of \(P\) in order to determine its Voronoi diagram. A point \(p \in P\) belongs to the facet \(F\) that minimizes its orthogonal6 distance to \(p\). Let \(f_F \colon P \rightarrow [0, \infty), p \mapsto f_F(p)\) denote the orthogonal distance of \(p \in P\) to \(F\) and let \(f \colon P \rightarrow [0, \infty), p \mapsto \min_F f_F(p)\). The point \(p\) belongs to the Voronoi cell of \(F\) if \(f_F(p) = f(p)\). That is, the function graph of \(f\) is piecewise linear and projecting its faces onto \(P\) gives the set of Voronoi cells resp. the Voronoi diagram of \(P\). Also note that each Voronoi cell is a convex polyhedron itself.
Algorithm. Let us consider for each \(F\) the half-space \(H_F\) in \(\mathbb{R}^{d+1}\) that contains \(P\) and whose boundary supports the function graph of \(f_F\). Computing the function graph of \(f\) is equivalent to intersecting the half-spaces \(H_F\). Using duality between points and hyper-planes, the convex hull algorithm by Chazelle7 solves this problem in optimal \(O(n^{\lceil\frac{d}{2}\rceil} + n \log n)\) time.
Concluding remarks.
As a side product, one obtains that the combinatorial size of the Voronoi
diagram is at most \(O(n^{\lceil\frac{d}{2}\rceil})\). For convex
polyhedra, the straight
skeleton, Voronoi diagram
and medial axis are equal. In fact,
the above technique has already been
applied to compute the
straight skeleton in the plane by consider lower envelopes of (partially
defined) linear functions. For straight skeletons of general input, however,
the difficulty is to construct for each linear function its individual domain
such that the lower envelope representation works out. For convex polygons, the
domain becomes trivial, as illustrated above. Also, to compute the Voronoi
diagram of points, Chazelle transforms the problem to intersecting half-spaces.
In fact, it would not be too surprising, if the result mentioned above can
be found somewhere in the literature. If you know of any reference, I would be
glad if you could tell me.
I would like to thank Anna Lubiw for mentioning this problem.
Update. Anna Lubiw informed me that in a technical report Mitra and Hafer8 used basically the same technique to solve this problem.
-
In discrete geometry, typically the Voronoi diagram of a finite point set is considered. In computational geometry, also (generalized) Voronoi diagrams of line segements or circular arcs are of interest, as they possess a vast number of applications. ↩
-
For convex polyhedra \(P\), the Voronoi diagram outside \(P\) is boring. ↩
-
A convex polyhedron in \(d\)-dimensional space is the convex hull of finitely many points, or, equivalently, the bounded intersection of finitely many half-spaces. We may assume here that the polyhedron does not reside within a lower-dimensional sub-space. Also note that no \((d-2)\)-dimensional face \(F\) of \(P\) is flat in the sense that if we take a point \(p\) of \(F\) then a local neighborhood of \(p\) on \(P\) does not reside within a \((d-1)\)-dimensional sub-space. ↩
-
A facet is a \((d-1)\)-dimensional face. ↩
-
We consider the infimum-distance between compact point sets. ↩
-
As we consider convex polyhedra, the infimum distance is equal to the orthogonal distance. ↩
-
B. Chazzelle, An Optimal Convex Hull Algorithm in Any Fixed Dimension, Discrete Computational Geometry, 10:377-409 (1993). ↩
-
P. Mitra and L. Hafer, Efficient Computation of the Medial Axis, School of Computing Science Simon Fraser University, B.C, Canada, 1998. [link] ↩