Skeletons and offsetting: A topological point of view
Abstract. We investigate topological properties of skeleton structures of shapes like Voronoi diagrams and straight skeletons. We show that these skeleton structures are homotopy-equivalent to the original shape and discuss the homology of skeletons in arbitrary dimensions. Motivated by applications in NC-machining, we investigate offset curves and their evolution and put it into context of persistent homology. One application is the generalization of maximum inscribed circles.
Update: A conference paper on this topic
appeared at EuroCG 2018.
Update: A related paper on this topic
appeared at iDSC2020.
Introduction to skeletons
Skeleton structures of plane shapes are line structures that represent this shape in some sense. They are typically computed as an intermediate data structure for many geometry-flavored algorithms in CAD, GIS, computational biology, mathematical origami, robot-motion and NC-tool path planing, and so forth. In this article we deal with the following two prominent examples of skeletons: The Voronoi diagram and the straight skeleton.
Voronoi diagram. Let \(P\) denote a polygon in the plane. We consider vertices and edges that constitute the boundary of \(P\), or faces1 for short. The (generalized) Voronoi diagram \(V(P)\) is a line structure that induces a tessellation of \(P\) into (Voronoi) cells such that each cell belongs to a face and consists of all points that are closest2 to this face.3
We can extend this definition straightforward to polygons with holes or polyhedral shapes4 in any dimension, e.g., a polyhedral torus. Especially in the CAD/CAM domain generalizations to polygonal shapes where the boundary elements are not only straight-line segments but circular arcs are of particular interest.
In the remainder of helps to mention the following technical details on the structure of the Voronoi diagram \(V(P)\) of a polygon with holes \(P\): The nodes on the boundary of \(P\) have degree one. In particular, we consider the two Voronoi edges emanating at reflex vertices of \(P\) to end at degree-1 nodes sitting on the same location. Parabolic edges of \(V(P)\) are split up by a degree-2 node at the apex, if contained. All other Voronoi nodes in the interior of \(P\) have degree three. (Nodes of higher degrees are split up into multiple nodes of degree three that sit on the same location.)
Straight skeleton. Let \(P\) denote a polygon in the plane. We consider the edges to move inwards at unit speed in a self-parallel manner. This wavefront propagation causes structural changes in the wavefront: (i) an edge may collapse, vanishes and the neighboring edges become adjacent or (ii) a reflex5 vertex may crash into another part of the wavefront causing the wavefront to split up. Eventually, the wavefront entirely collapsed and vanished entirely.
The straight skeleton is the line structure that is traced out by the moving wavefront vertices. Also the straight skeleton tessellates the polygon into cells6 and each cell belongs to an edge of the polygon.
There are various generalizations of straight skeletons: (i) there are different attempts to generalize straight skeletons to three or higher dimensions, (ii) for weighted straight skeletons different speeds of the edges are considered, (iii) different initial wavefront patterns at reflex vertices (or terminal vertices) lead to the so-called linear axis. An overview is given in my thesis.
Topology of skeletons
As mentioned, the Voronoi diagram and the straight skeleton of some input captures features of the shape of the input. We can make this statement precise by saying that the Voronoi diagram and straight skeleton of a polygon with holes, \(P\), has the same homotopy type as \(P\), and in this sense encode the topology of \(P\). This can be easily seen as follows.
Homotopy type
Deformation retraction. The main claim is that there is a deformation retraction of \(P\) to its Voronoi diagram and straight skeleton, which makes them all homotopy-equivalent.
In two dimensions, each straight skeleton cell \(C_S(f)\) of a face \(f\) of \(P\) is topologically a disk, i.e., it has no holes. A connected part of the boundary of \(C_S(f)\) is \(f\) itself. Let us denote by \(S(P,f) = S(P) \cap C_S(f)\) the boundary of \(C_S(f)\) without \(f\). Then \(S(P,f)\) is also a connected part of the boundary, and hence, there is a deformation retraction of \(C_S(f)\) to \(S(P,f)\). We can plug these retractions together in a way that we obtain a deformation retraction of all faces \(f\) of \(P\) to their respective \(S(P,f)\) and \(\bigcup_f S(P,f) = S(P)\), i.e., we obtain a deformation retraction of \(P\) to \(S(P)\). From this deformation retraction the homotopy-equivalence \(P \simeq S(P)\) follows.
Positively weighted straight skeletons behave in this respect the same as unweighted straight skeletons, cf. [Bie*15].
For Voronoi diagrams in the plane essentially the same argument applies. However, at reflex vertices \(v\) we need to refer to the technical detail mentioned above that the two Voronoi edges emanating at \(v\) are not connected at \(v\), they are only geometrically embedded in a way to intersect at \(v\). That is, as a topological space \(V(P)\) could be constructed by gluing together edges at Voronoi nodes, but we do not glue at reflex vertices.
Another way to approach the technicality at reflex vertices is the following: We perturb \(P\) a bit by replacing reflex vertices by tiny circular arcs that are tangential to the edges incident these vertices and receive the shape \(\widehat{P}\) with \(P \simeq \widehat{P}\). Then \(V(P)\) and \(V(\widehat{P})\) are just perturbed geometric embeddings of the same structure, i.e., \(V(P) \simeq V(\widehat{P})\), if the structural properties at reflex vertices are taken into account. Finally we can apply the above proof idea for \(\widehat{P} \simeq V(\widehat{P})\) without the technical complications at reflex vertices. Plugging the homotopy-equivalences together we get \(P \simeq V(P)\).
In higher dimensions we can do the same7: We retract each Voronoi cell \(C_V(f)\), which is topologically a ball, to \(V(P,f)\), which is topologically a ball one dimension lower that lives on the boundary of \(C_V(f))\), and plug these per-cell retraction together to a deformation retraction of \(P\) to \(V(P)\).
By the way, since the medial axis \(M(P)\) of a polygon with holes, \(P\), is the same as the Voronoi diagram \(V(P)\) only with the edges emanating at reflex vertices removed, we see that \(P \simeq V(P) \simeq M(P)\).
Negative examples. Interestingly, an arbitrarily weighted straight skeleton behaves differently as shown in [Bie*15]: With negative weights the straight skeleton can have loops even if \(P\) is a simply polygon. (The above proof does not apply because the cells are not confined to \(P\).) This observation puts a question mark to the “skeleton” in “arbitrarily weighted straight skeleton”, as I personally prefer to think of a skeleton in the following way:
Definition of a skeleton. A idea behind a skeleton seems to be a condensed representation of a shape that is advantageous for further analysis or processing. Following this guidline I would define a skeleton of a polyhedral shape as follows.
A skeleton of a polyhedral shape \(P\) in \(d\)-dimensional space is a \((d-1)\)-dimensional deformation retraction of \(P\).
Using this definition of a skeleton we then arrive at this statement:
The Voronoi diagram, the medial axis and the positively weighted straight skeleton are skeletons of polyhedral shapes.
Homology
Homotopy-equivalent spaces have isomorphic homology groups.8 As a consequence, the homology groups of \(P\), \(V(P)\) and \(S(P)\) are isomorphic.
That means, the Voronoi diagram and the straight skeleton of a simple polygon \(P\) is a tree. (This is well known, but the above topological argument appears very appealing to me. The argument is essentially based on topological arguments.) Moreover, for each hole that we cut out of \(P\) the Voronoi diagram (straight skeleton, resp.) gets a “new” cycle, that is, a new “generator cycle” in a free abelian group of “cycles”, namely the Homology group \(H_1(P)\). In three-dimensional space, the Voronoi diagram (or straight skeleton7) of a solid torus with a ball cut out is topologically a sphere \(S^2\) with a cycle \(S^1\) attached.
By Euler–Poincaré the Euler characteristics of \(P\) and its skeletons are identical.
Offsetting
From a topological point of view the straight skeleton and the Voronoi diagram, or skeletons in general, are the same; the difference is of geometric nature. This geometric difference can be seen in the offset curves that belong to each skeleton.
Two geometries of offset curves
Given a polygon with holes, \(P\), suppose we would like to inset \(P\) by some radius \(r\) such that if we fill out the inset shape with a pen of this radius, we basically get \(P\) (except that this pen cannot get into corners, for instance). Mathematically speaking, we would like to find a shape \(Q_r\) (or its boundary curve) such that the Minkowski sum \(Q_r \oplus D_r \subseteq P\), with a disk \(D_r\) of radius \(r\) centered at the origin, is the largest possible within \(P\). In GIS this concept is known as a buffer and in CAD it is known as offsetting.
Minkowski-difference. Mathematically speaking, we could ask for the Minkowski difference \(P \ominus D_r\) of \(P\) with the disk of given radius \(r\). The Minkowski difference at a reflex vertex of \(P\) is formed by a circular arc.
Mitered offet curve. When a tool of an NC-milling machine is following this circular arc then this reflex vertex will remain but imperfections of the tool path accuracy will erode this corner. One could remove the circular arc by extending the adjacent line segments and still obtain a tool path that gives the original reflex vertex, i.e., the Minkowski sum with a disk of given radius is still the same. The resulting offset curve is often called mitered offset curve.
One could also replace this one vertex in the offset curve with a few more and obtain something “between” these two extreme cases. This leads to the linear axis9, which is also a skeleton.
Computing offset curves
Computing offset curves “brute force” is a notoriously difficult and error-prone task. If the radius \(r\) is small then the task is trivial; one just moves the elements of the boundary of \(P\) inwards by \(r\). However, when \(r\) grows then first only structural (e.g., one element vanishes) but soon topological changes (e.g., the curve splits up) occur.
It is worth to consider the evolution of the offset curves for \(r\) ranging from zero to infinity. The next figure shows first the Minkowski-difference version and then the mitered offset curve. (The third version with the linear axis would lead to the previously mentioned multi-vertex offsets around reflex vertices of \(P\).) In order to show the connection to skeleton structures, the figure also depicts the Voronoi diagram and the straight skeleton: The offset curve within a skeleton cell \(C(f)\) is determined by \(f\) only.
If the skeleton of \(P\) is already known then the computation of a single offset curve for any given radius \(r\) is simple, efficient (linear time) and numerically stable. All one has to do is to traverse the skeleton in a certain way and insert element by element of the offset curve. This is exactly what the software packages (Arc)Vroni and Stalgo do. See §1.3.1 in my thesis for further details.
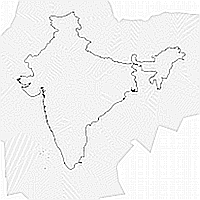
The following figure illustrates a more complex (set of) polygons. Computing straight skeletons is P-complete10 and we do not know how to efficiently compute an offset curve (e.g., choose one in the middle of a India) without essentially knowing the skeleton (or something similar to knowing the whole evolution of the offset curves). See the website of Stalgo for its straight skeleton.
The skeletons are the “interference patterns” of the wavefront propagation formed by the offset curves. Straight skeletons are originally defined by offset curve (wavefront) propagation. For Voronoi diagrams, this is known as the grass fire model of Voronoi diagrams. (Fun fact: For certain input polygons and metrics the Voronoi diagram and the straight skeleton are actually the same simply because the wavefronts are the same. This observation was exploited in [Hub*14] to generalize straight skeletons to arbitrary dimensions.) To sum up, we can go from skeletons to offset curves and from the evolution of offset curves back to skeletons. They are in a one-to-one correspondence.
The geometric difference of those two skeletons, in this sense, can be visualized or manifests in the different geometries of the offset curves. Since the skeletons are homotopy-equivalent, the differences in the evolution of the offset curves are “only” of geometric nature. And still, in the plane we can compute a Voronoi diagram in optimal \(O(n \log n)\) time, but for straight skeletons the best algorithms are a factor \(\sqrt{n}\) slower and we just hope that \(O(n \log n)\) may be achievable in theory.
Persistence
The evolution of offset curves directly leads to the concept of persistence in computational topology. Let us consider the inset polygon \(Q_r\) (in the Voronoi diagram or straight skeleton way). With \(r\) ranging from \(\infty\) to \(0\) we get a sequence of growing sets \(Q_r\) from the empty set to \(P\), which is called a filtration. Persistent homology tracks the evolution of the homology groups – the birth and death of homology classes – during the evolution of \(Q_r\) in the filtration. In two dimensions, at certain discrete points in time components (0-dimensional homology classes) of \(Q_r\) are born and die (get merged), and holes (1-dimensional homology classes) of \(Q_r\) are born and die (get filled). (In our case, the latter does not really happen as we will see.)
Construction of the filtration. Lets make the outline above more precise. First of all, we do not consider the continuous growth of \(Q_r\) with \(r \searrow 0\) but only at those finitely many points in time mentioned above, i.e., at those points \(r_1 \ge \dots \ge r_k\) in time where the boundary of \(Q_{r_i}\) hits a node of the skeleton. We have \(r_k = 0\) and therefore \(Q_1 \subset \dots \subset Q_{r_k} = P\).
Secondly, we need a simplicial complex that models \(P\), i.e., a (topological) triangulation of \(P\). We obtain a filtration by starting at the empty set and then adding simplices in way that we get a sequence of sub-complexes. However, we would like to see (triangulations of) \(Q_{r_i}\) in the filtration. So we actually consider the offset curves formed by the boundaries of \(Q_{r_1}, \ldots, Q_{r_k}\) which form nested onion layers and then we triangulate the space between the onion layers. The filtration then starts at the empty set and we add for each \(r_i\) those simplices between \(Q_{r_i}\) and \(Q_{r_{i-1}}\).11
Roof model and super-level set filtration. Another perspective to the construction above is to consider the super-level set filtration of the roof model of the skeleton. We call \(T_S(P) = \{\text{bd } Q_r \times \{r\} \colon r \in [0, \infty) \}\) the roof model of the straight skeleton \(S(P))\), and analogously for the Voronoi diagram \(V(P)\). That is, we embed the shrinking process of the offset curves into three-space, where the third coordinate is time. The level set of \(T(P)\) at level \(r\) is an offset curve \(\text{bd } Q_r\) and the super-level set is \(Q_r\) itself. The super-level set filtration is the filtration obtained by the super-level sets with descending level \(r\). This is exactly the filtration described above, where the triangulated roof \(T(P)\) was refined by the level set. In the filtration the simplices in the belt between two consecutive level sets are inserted at the same time (level).
Computing persistence. The standard algorithm for computing persistence is the boundary matrix reduction algorithm by Edelsbrunner and Harrer12. This is the algorithm implemented by libstick. It runs in \(O(m^3)\) where \(m\) is the size of the simplicial complex. The filtration we constructed above is defined on a simplicial complex with \(m \in O(n^2)\) simplices which leads to a runtime of \(O(n^6)\).
In two dimensions, we can do much better. We already observed that the skeleton tracks the evolution of the offset curves. More precisely, it holds that \(Q_r\) is homotopy-equivalent to \(S(P) \cap Q_r\) and \(V(P) \cap Q_r\). (We can see this by applying the same homotopy proof as for \(P \simeq V(P) \simeq S(P)\), but restricted to \(Q_r\).) That means the homology groups of \(Q_r\) evolve ismorphically to the homology groups of its skeletons.
That is, we could consider the skeleton mapped on the roof model. Birth and death of homology classes happens at skeleton nodes.13 We then consider the super-level set filtration on the skeleton. This reduces the size of of the filtration from \(O(n^2)\) to \(O(n)\). Using the boundary matrix algorithm we can compute persistence in \(O(n^3)\).
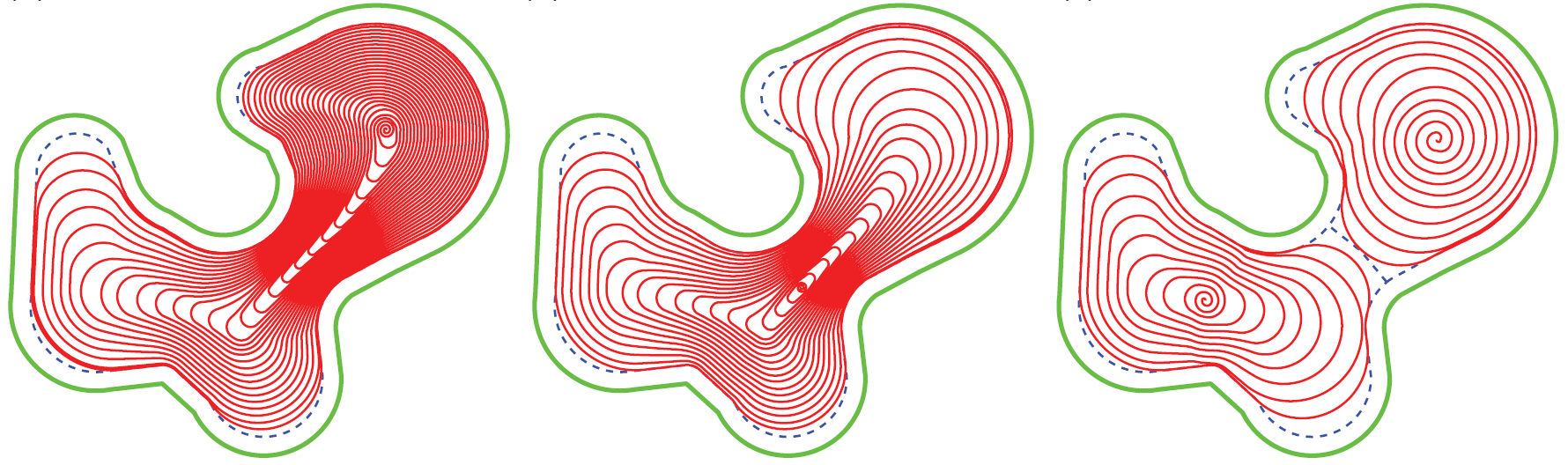
The below figure illustrates the evolution of the straight-skeleton offset filtration of a polygon with holes \(P\). The red circles mark the locations where 0-dimensional homology classes are born (the label contains the order and time of birth). The purple crosses mark the time of death of a 0-dimensional homology class; the grey arrows show which class died by being merged to which class. The orange circles mark the birth of a 1-dimensional homology class.
An efficient algorithm. In the case of offset filtrations, we can compute peristence in \(O(n \alpha(n))\) time. The key observation is that there are no local minima in the roof models. Hence, cycles never die. We can always follow the gradient downwards until we hit the boundary of \(P\) at level \(0\). Hence, in oder to compute the 0-th and 1-st persistent homology groups, it suffices to use a union-find data structure whose operations are in \(O(\alpha(n))\).
We assume that all nodes have degree three, except for those on the boundary of \(P\), which have degree one. (This is not an essential restriction, it only makes the presentation simpler.) We put all nodes of the skeleton in a priority queue and process them with descending level. When a node is processed with all neighboring nodes having a lower level then we make a new component. When a node is processed with exactly one neighbor having higher level then we merge it with the one component. When a node is processed with two neighbors having a higher level, we have two cases: (i) they belong to different components, and we merge the younger one with the older one, i.e., the younger homology class dies. (ii) the nodes belong to the same component, and a 1-dimensional homology class is born, which never dies. The case where all three neighbors would have a higher level cannot happen as this would indicate a local minimum in the roof model.
If the skeleton of \(P\) is given we can compute the persistent homology groups of the offset-curve filtration of \(P\) in \(O(n \alpha(n))\) time.
Maximum inscribed circle. An illustrative application of the Voronoi diagram (or medial axis) is the computation of the maximum inscribed circle of a polygon with holes \(P\) in \(O(n)\) time. The center of the maximum inscribed circle needs to lie on a node of \(V(P)\): The maximum inscribed circle has to touch the boundary of \(P\) at least at three points. These three points belong to different faces of the boundary of \(P\) and there is no face that is strictly closer to the center. Hence, the center lies on a Voronoi node that is shared (at least) by the cells of the three faces that contain the three points. The distance of a node to its defining faces is called its clearance.
The Voronoi diagram has \(O(n)\) nodes, so we can find the node with the largest clearance in \(O(n)\) time; it is the center of the maximum inscribed circle.
In the roof model the maximum inscribed circle is the highest peak, the global maximum.14 The height of the node is its clearance. Maybe we are not interested only in the maximum inscribed circle, but in a couple of “large” inscribed circles that depict the “main parts” of the shape. It is easier to state this in the roof model: We may not only be interested in the global maximum but in all “significant” peaks. As an example in NC-machining, consider the Voronoi-based high-speed pocket machining paths computed by Held and Spielberger, where they decompose shapes into its “main parts”:
The notion of “significance” of a peak can be made precise by the persistence of the 0-th dimensional persistent homology classes, which is the difference of the time of birth of a peak and the time of death, i.e., when it is merged with another peak. This is what the so-called persistence diagram illustrates. It illustrates all persistent homology classes as points, where the \(x\)-coordinate is the birth level and the \(y\)-coordinate is the death level. The significance is therefore the vertical distance to the main diagonal. The birth level is the radius of the corresponding inscribed circle. The maximum inscribed circle corresponds to the peak that is born first and never dies.
Below we see the 0-th dimensional persistence diagram of the straight-skeleton offset filtration resp. the super-level set filtration of the roof model. We clearly see that two homology classes have a particularly high peristence: the peaks 1 and 2. The homology class with the third-highest persistence was born quite late, at level 0.420, cf. peak with label 6 in the figure above showing the evolution of the homology classes. (We reversed x- and y-axis to have time (birth- and death-levels) grow into the natural direction.)
Note that the local maximum with a high level but low persistence is not what we look for in the high-speed machining application. These are points in the persistence diagram with high birth level but which are close to the diagonal. We actually look for high-persistence peaks. A related article to this is about detecting peaks in a signal using persistent topology.
Bottleneck. Another application of the Voronoi diagram (resp. medial axis) is the detection of bottlenecks in a shape. The basic idea is that if we consider those parts of the Voronoi diagram that belong to the medial axis then a node with two edges incident where the neighboring nodes have higher clearance forms a bottleneck. A bottleneck with a clearance smaller than a value \(r\) cannot be passed by a disk-shaped tool of radius \(r\).
Persistence gives us a bit more information for this application. Consider for instance a polygon with holes \(P\), where one hole is moderately close to the outer boundary of \(P\). There is a bottleneck by the above definition; a tool cannot pass this bottleneck. However, it may be able to get to the other side by another path.
Assume that a 0-dimensional homology class dies lately, i.e., after level \(r\). That means one component merges with another, and a Voronoi node belongs to this event. A disk with radius \(r\) cannot move from the first component to the other. We can only move within the components of the inset shape \(Q_r\), but not between components that merge later (i.e, at lower levels) than \(r\). The number of components of \(Q_r\) is the number of points in the persistence diagram in the upper-left quadrant with origin at \((r, r)\) on the diagonal. Every such point is a component that is born at a level above \(r\) and death level below \(r\).
References
This article deals with algorithms and mathematical formalisms that belong to the field of computational topology. The introduction to this field is the book by Edelsbrunner and Harer12.
-
As usual in discrete geometry a face of a \(d\)-dimensional polyhedron is a boundary element of arbitrary dimension, whereas a facet is a face of dimension \(d-1\). ↩
-
We refer to Euclidean infimum distance between point sets here. But Voronoi diagrams were generalized to different metrics as well. Indeed Abstract Voronoi Diagrams were defined by Klein et alii where, essentially, the metric (or “geometry”) was removed. ↩
-
Generally speaking, a Voronoi diagram of objects in an ambient space tessellates the ambient space into Voronoi cells, each cell belonging to one object, containing the points closer to this object than to all other objects. This point of view would make it more natural to speak of \(V(\mathcal{F}(P))\), where \(\mathcal{F}(P)\) would be the face set of \(P\). But in this article we think of \(V(P)\) being a skeleton of \(P\). However, also in this interpretation we associate to each face a cell, but some cells are trivial, i.e., they encompass its face only. ↩
-
Let a polyhedral shape be defined as a bounded set in Euclidean space whose boundary is a manifold one dimension lower consisting of polyhedra. A polyhedron is homeomorphic to a ball; it possesses no holes. (If you construct a torus by removing a prism from a cube such that cube facets get holes then you need to add additional edges.) ↩
-
A vertex is reflex if the inner angle is larger than 180°. ↩
-
The cells induced by the straight skeleton are commonly known as “faces”, but we use the term “cell” here. ↩
-
Some approaches to generalize straight skeletons to higher dimensions have some pitfalls, so we could at least consider this as a strong property we request from any reasonable generalization of straight skeletons to higher dimensions. ↩ ↩2
-
See for instance corollary 2.11 in Hatcher or IV.2 in Edelsbrunner and Harer. ↩
-
See M. Tănase and R. C. Veltkamp, A Straight Skeleton Approximating the Medial Axis, ESA ’04, pages 809–821, Bergen, Norway, Sep 2004. ↩
-
The straight skeleton is known to be P-complete and therefore “inherently sequential”, i.e., there seems to be no way around simulating the wavefront the one or other way. However, this argument does not apply to (generalized) Voronoi diagrams, for which efficient divide-and-conquer algorithms do exist. ↩
-
Actually, we keep adding simplex by simplex such that at we obtain a simplicial complex at any time, i.e., we add a simplex only after all its boundary elements were added. We bring the simplices in the onion layers in any order, but only for “formal” reasons, since we consider the insertion times to be all equal, so “inter-onion-layer” homology classes that are born also die at the same time and therefore have zero persistence. From persistence point of view they are irrelevant, they are depicted by dots on the diagonal of the persistence diagram, c.f. getting started of libstick. ↩
-
H. Edelsbrunner and J. Harer, Computational Topology. An Introduction, 2010, ISBN 0-8218-4925-5. ↩ ↩2
-
Recall that we split up parabolic edges at its apex. ↩
-
Of course, there could be more than one maximum inscribed circle, i.e., the global maximum in the roof model may not be unique. ↩